4.1 流动空气的特性 | 飞机在空中飞行,根据相对性原理也可以看成飞机周围的空气用同样的速度以相反的方向流过飞机表面。流过飞机表面的空气会对飞机产生作用,这种作用主要有两个方面:力学作用和热力学作用。也就是空气将加一种力在飞机上,称之为空气动力,同时由于空气分子与飞机表面的摩擦,将使飞机表面的温度增高。本章只讲座空气的力学作用,至于空气加热问题将在宇宙飞行器一章加以阐述。
为了研究空气动力的本质,必须了解流动空气的特性。但是要试验观察流动空气比较困难,人们用流动的液体来代替气体进行试验。因为液体和气体流动时的主要特性具有共同之处。.在一个容器中充满液体,把进口和出口的开关同时打开让液体从容器中经过剖面不等的管道流出,同时保持容器内液体表面的位置不变。这时流体的流动是不随时间而变化的,是稳定的。 | 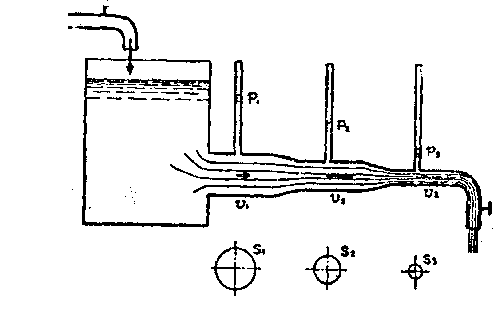 | | 如果流动的速度不太高,那么流体可以认为是不可压缩的即在流动过程中流体密度不发生变化。同时流体也不会中断,必须维持连续的流动。这样在单位时间内流过管道内不同剖面处的流体质量应该一致。若单位时间内流过剖面Sl处的流体质量为m1,流过S2处的为m2,流过S3处的为m3.于是有: |  | | 如果用表示时间内流过的流体质量。p表示流体密度,v表示时间t内流体流过的容积,S为管道剖面面积,l为时间t内流体流过的路程.则: | 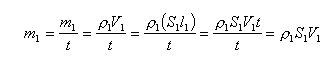
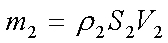
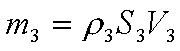 | 因为流体不可压缩,所以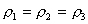 ,于是有: ,于是有: | 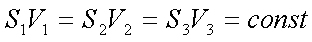 | 该式称为“连续方程式,'。由该方程可以得出如下结论:
当流体以稳定的流速在管道内流动时,管道剖面小的地方流速大,而管道剖面大的地方流速小。即: | 
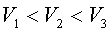 | | 在上述流体实验装置中,不同剖面的管道上还装有液体压强计,从压强计内液面的高低可以读的不同剖面的管道内流体静压的大小.实验表明:在管道剖面大的地方,流体的静压也大,在管道剖面小的地方,静压也小,用p表示静压,于是上述关系表示为: | 
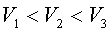
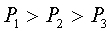 | | 1783年瑞士物理学家伯努利首先导出不同剖面的管道内流体的流速和静压的关系: | 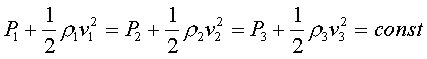
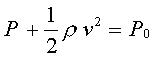 | | 该式称为“伯努利定理!'(Berroulli's theorem)。 |
|
|
|
|

